![]()
Finding side lengths
Example 1
Find the value of x, correct to 4 decimal places, in each of the following:
- This problem involves opposite and adjacent so use tangent.
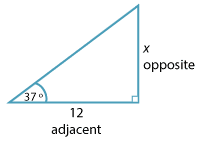
Detailed description \begin{align}\dfrac{x}{12} \ &= \ \text{tan} \ 37° \\ x \ &= \ 12 × \text{tan} \ 37° \\ &\approx \ 9.0426\end{align} - This problem involves adjacent and hypotenuse so use cosine.
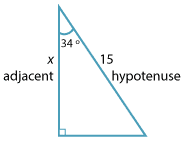
Detailed description \begin{align}\dfrac{x}{15} \ &= \ \text{cos} \ 34° \\ x \ &= \ 15 × \text{cos} \ 34° \\ &\approx 12.4356\end{align} - This problem involves opposite and hypotenuse so use sine.
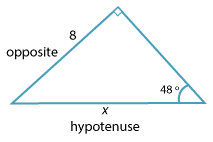
Detailed description \begin{align}\text{sin} \ 48° \ &= \ \dfrac{8}{x} \\ x \ × \ \text{sin}\ 48° &= \ 8 \\ x \ &= \dfrac{8}{\text{sin} \ 48°} \\ &\approx 10.7651\end{align}




